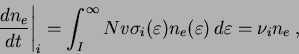 |
(2.7) |
An electrical discharge is produced when gas molecules or atoms are ionized by electron impact. In the absence of losses, the change in the electron density is given by:
where the subscript ![]() denotes that this is an electron
density change due only to electron impact ionization,
denotes that this is an electron
density change due only to electron impact ionization, ![]() is
the ionization cross section by electrons with energy
is
the ionization cross section by electrons with energy ![]() ,
,
![]() is the free electron density as a function of
energy,
is the free electron density as a function of
energy, ![]() is the ionization potential energy, and
is the ionization potential energy, and ![]() is the
ionization frequency (the average number of ionization events per
electron per second). The ionization potentials for the two major
constituents of air, N
is the
ionization frequency (the average number of ionization events per
electron per second). The ionization potentials for the two major
constituents of air, N![]() and O
and O![]() , are 15.6 eV and 12.2 eV
respectively.
, are 15.6 eV and 12.2 eV
respectively.
Assuming that ![]() is constant, the solution to Equation
2.7 is
is constant, the solution to Equation
2.7 is
| (2.8) |
where ![]() is the initial electron density. In the
absence of losses, the electron density increases exponentially with
time.
is the initial electron density. In the
absence of losses, the electron density increases exponentially with
time.
After an ionization event, a free electron can ``recombine'' with a positive ion. In the absence of other processes, the change in the electron density due to recombination is given by:
where ![]() is the electron-ion recombination coefficient,
is the electron-ion recombination coefficient,
![]() is the positive ion density, and the subscript
is the positive ion density, and the subscript ![]() indicates
that this is an electron density change due only to recombination. If
one assumes that the plasma is neutral with only single ionization,
then
indicates
that this is an electron density change due only to recombination. If
one assumes that the plasma is neutral with only single ionization,
then ![]() . Substituting into Equation 2.9
and solving for
. Substituting into Equation 2.9
and solving for ![]() gives:
gives:
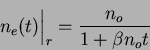 |
(2.10) |
In addition to recombining with positive ions, electrons can also
attach to neutral molecules if the gas has electronegative properties.
Air is an electronegative gas because of the electron affinity of
![]() . Electrons can attach to oxygen either in triple collisions (
. Electrons can attach to oxygen either in triple collisions (
![]() ) or via dissociative attachment
reactions (
) or via dissociative attachment
reactions (
![]() ). The latter form
of attachment dominates at
). The latter form
of attachment dominates at ![]() values near that of breakdown. The
change in electron density due to attachment is:
values near that of breakdown. The
change in electron density due to attachment is:
giving:
| (2.12) |
where ![]() is the attachment frequency.
is the attachment frequency.
At ![]() values near breakdown, electron loss is due primarily to
attachment processes and in particular to dissociative attachment
(Bazelyan and Raizer, 1997, p. 24). At a given
values near breakdown, electron loss is due primarily to
attachment processes and in particular to dissociative attachment
(Bazelyan and Raizer, 1997, p. 24). At a given ![]() value, both the
ionization and attachment frequencies will be proportional to the air
number density,
value, both the
ionization and attachment frequencies will be proportional to the air
number density, ![]() , since the collision rate is proportional to
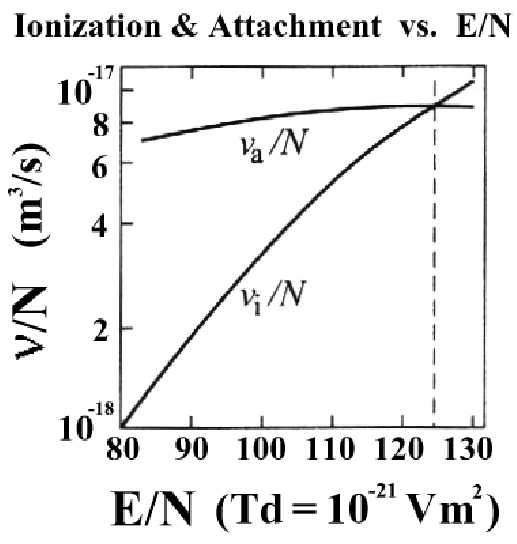
, since the collision rate is proportional to ![]() (see Equation 2.3). Figure 2.1 shows the
density-normalized ionization frequency (
(see Equation 2.3). Figure 2.1 shows the
density-normalized ionization frequency (![]() ) and attachment
frequency (
) and attachment
frequency (![]() ) plotted as a function of
) plotted as a function of ![]() in units of
Townsends (
in units of
Townsends (![]() Td
Td
![]() V
V![]() m
m![]() ). For any given N, the
ionization frequency will exceed that of attachment when
). For any given N, the
ionization frequency will exceed that of attachment when
![]() Td. This is the basis for the breakdown strength of air
at standard temperature and pressure (STP). An
Td. This is the basis for the breakdown strength of air
at standard temperature and pressure (STP). An ![]() of 123 Td
corresponds to a breakdown field of
of 123 Td
corresponds to a breakdown field of ![]() MV/m at STP.
MV/m at STP.
 |